如何正確使用賽局理論來推導「防疫策略」?/Vivian Fang
最近疫情肆虐,各國因應方法不一;有些靠經驗、有些靠佛心,但也有人試圖用學術方法,推導出合理的、將損害壓到最低的策略。「賽局理論」也是這些學術方法之一,但遺憾的是,部分相關的論述方式並不準確。
筆者忝為教授賽局理論的老師,就以本文來說明一下在這個題目上的應用方式、以及為什麼「謹慎防疫」應該是目前最適合台灣的策略。
以賽局理論看防疫策略
在某篇日前被廣傳的「以賽局理論分析防疫」文章中、以及一些其他類似作品中,都有個很大的問題,就是將賽局中的「策略」(strategy) 和可能的「結果」(outcome)混為一談,而這兩者其實是完全不同的概念。
事實上,在筆者以賽局矩陣表(payoff matrix)解釋該文的數字設計、並以賽局理論工具正確推導出來的結論,竟然跟該文想表達的論點恰恰相反。
賽局中的「策略」和「結果」是完全不同的概念。
例如該文提到「全面防堵或是全面減災都是辦不到的事」,但用它的賽局架構推導出來的結論,跟這句話竟然是自相矛盾的。
由於這篇推導有問題的文章受到廣傳,所以或許讀者對賽局理論是有興趣的,所以筆者寫下這篇文章,說明賽局理論的適當應用方式、以及比較正確的觀念。
在本文中,筆者會以武漢肺炎(新冠肺炎、COVID-19)防疫時事為題目,以賽局理論架構中的「賽局矩陣表」(game matrix)架構及工具,來拆解目前面對防疫局勢的策略。
賽局理論入門
先來談談賽局入門(熟悉的人不妨跳過)。賽局的基本要素包括:
玩家(player):玩家必須多於一人,兩人才能成局的概念。
策略(strategy):指的是在所有可能發生情況下的一套完整行動計畫;這完全決定了玩家的行為。
得失/支付(Payoffs): 「得失」指的是賽局裡玩家在每個可能的行動的「得」與「失」;簡單來說,可以想成玩遊戲裡的「得分」。由於這個「得失」取決於對手玩家的策略,學術上一般以支付(payoffs)的函數來計算。
最佳反應(Best Respond,以下簡稱BR):針對「對手玩家」的某一策略,能帶給此玩家最佳「得失」(payoff)結果的策略,就是「最佳反應」。換個角度想,最佳反應(BR)問的就是:「當對手出某一招時,你出哪一招才能才會高分?」
均衡(Equilibrium):均衡就是平衡,也是最終的賽局結果。在賽局裡一般簡單的均衡指的是「納許平衡」(Nash Equilibrium)。
防疫策略賽局
好,介紹完基本因素之後,現在進入正題,來談談防疫策略的各種計算條件。
假設:
兩位玩家:A國與B國;
兩個策略:「封鎖」 (Lock-down)或「防疫 」(Containment,也就是不封鎖,但在必要時管制特定行為);
兩位玩家在下列條件上都有相似背景:醫療資源、人文、政治態勢、經濟體系及規模,而且目前皆處在「未爆發重度社區感染」的狀態;
另外還包括兩個假設:
4. 採取「封鎖」策略時的得分:
如兩位玩家都同時採取「封鎖」策略,成本為80,得分為-80分(因為是負面結果,所以分數為負分);
如果單方採取「封鎖」策略,因為封鎖的一方必須加派人員,防止對方人員入境,所以成本為100、得分為-100分。
5. 採取「防疫」策略的得分:
如果兩位玩家同時採取「防疫」策略,成本為40,得分為-40分;
如果單方採取「防疫」策略,因為還得加派醫療人員,協助追蹤境外移入感染,所以成本為60,得分為-60分
從上述的得分設計,可以看出此賽局假設中的「防疫」成本比「封鎖」低。
當然,「防疫」策略對醫療體系造成的衝擊、以及社會成本也都很高;但畢竟「封鎖」的先期成本(軍方、官方、海關等)相對高,更不用說可能造成的恐慌效應,以及企業、勞工等其他社會成本了。
所以,將「封鎖」成本設定得比較高,應該是合理的假設。
賽局矩陣
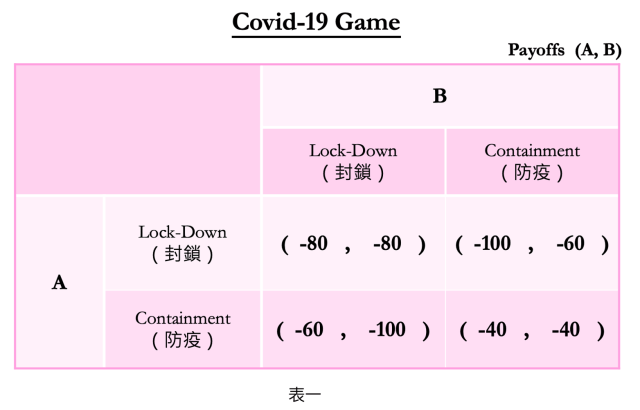
此賽局有2位玩家、雙方有2個可選用的策略,所以共有 4個可能發生的結果(outcome);而賽局矩陣(game matrix),就是將玩家的得分(payoffs)放入一個2x2的表格,如表一示意。
玩家的得分(payoff)讀法是,每一格的左邊數字代表國家A的分數,右邊的是國家B的分數,如表右上標示的定義。
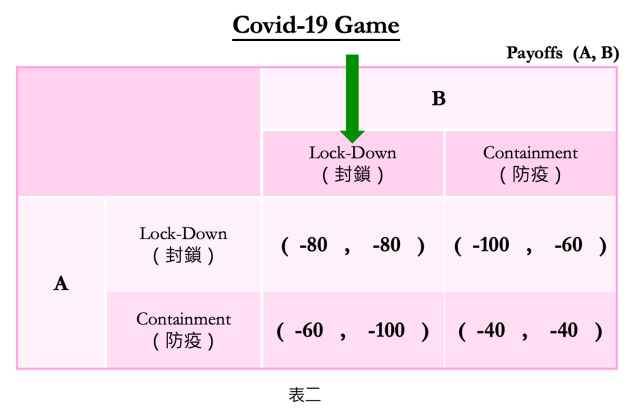
那麼,就讓我們用賽局矩陣的小技巧,來拆解國家A的最佳反應(BR):當國家B採取「封鎖」策略時,請看表二的左欄中,圖示的綠色箭頭處:
從表二可知:國家A採取「封鎖」策略的得分為-80,採「防疫」策略的得分為-60;而因為-60大於-80,所以當國家B採用「封鎖」策略時,國家A的最佳反應應該是「防疫」。
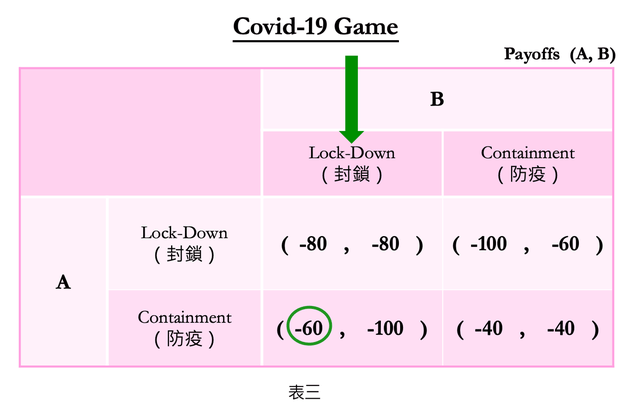
在賽局矩陣中,將高分數字圈起來就代表是最佳反應分數,如表三中的綠圈:
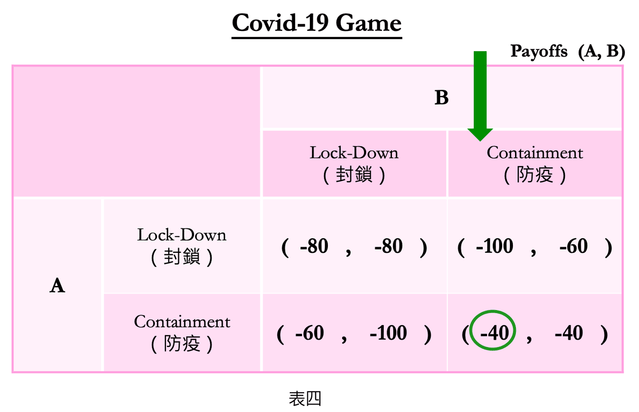
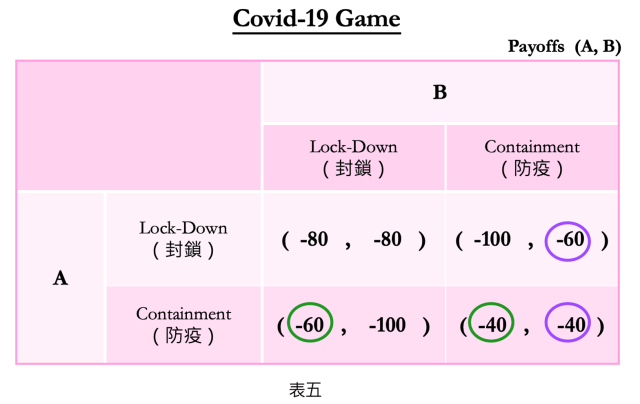
而如果國家B採「防疫」策略,則請看表格中的右欄。用同樣計算方法,在表四中可以看到-40大於-100,所以國家A的最佳反應一樣是「防疫」。所以我們將把最高分圈起來,如表四右邊的綠色圓圈:
這邊先再介紹一個賽局新名詞「優勢策略」(dominant strategy):不管對手出哪一招,只要玩家出這招都可以拿高分,就叫做優勢策略。
而由於不論國家B採哪個策略,國家A都是「防疫」分數高,所以「防疫」就是國家A的優勢策略。
依照同樣的方法來分析國家B的策略,這邊就不重複過程了;結果如表五所示:
用紫色圈出來的,就是國家B的最佳反應;從圖中不難發現,國家B的優勢策略一樣也是採取「防疫」措施。
畫圈圈這個賽局技巧,是用來幫助尋找均衡點;當矩陣裡每位玩家的最佳得分都被圈出來,就代表找到了賽局終點。
當有個「可能的賽局結局」 (possible outcome)是雙方都獲得最佳反應時,賽局就找到了稱為「納許均衡」的平衡點,也就是雙方都應該理性採取「防疫」策略。
結論:兩國都應該採「防疫」策略,而非「封鎖」策略。
結語
當然,上述的賽局模型簡化了很多其他可變的因素及參數,也假設了政府有能力追蹤每一位入境者的旅遊史和感染史,而且醫療體系也尚足夠應付。
此賽局也只探討靜態(static game),實際上這些情勢隨時在變化,應該是動態賽局(dynamic game);不過,這個簡單的賽局分析結論,剛好呼應了台灣當局目前的策略。
在社區疫情未大爆發前,應該採取的是「防疫」策略;包括審慎查詢每一位確診案例染症來源、追蹤確症個案接觸人士、謝絕疫情嚴重區之入境、並加強自疫區返國人士的自我居家管理,以隔離患者、杜絕傳染。
如果是未染症的國人,則最好能勤於洗手、出入人多場合時戴口罩、延緩舉辦大型活動、減少外出等等,透過這些措施來自我保護,應該相對比「全面封鎖」來得理智。
上述的賽局理論分析,也說明了對台灣而言,現階段「嚴謹防疫」應該是目前最理想的策略。
參考閱讀
〈逃之夭夭〉:此篇談及「策略」、「possible worlds」等面向。
〈又毀了?〉:此篇談的是賽局的結果(outcome)。
〈Just Do It (JDI)-1 〉:此篇針對最佳回應(Best Respond)提供了介紹及案例。