從數學到計算思維、科學方法／洪士灝

下圖是小孩和我討論的國中數學題目。直覺上，大家會認為邊長較大的三角形面積較大，但真的是這樣嗎？原出題者可能想顛覆這個想法，或是看看考生是否會多想想。

然而，不知道是否為了容易計算，或者為了增加戲劇性，題目特別找了兩組數字，拼湊出面積相同的答案。小孩算出答案後，馬上自作聰明的說：「喔，如果等腰三角形的腰相等，面積就相等」。

我說，不要那麼快下定論。我們先拿出圓規直尺出來做實驗，畫出好幾個腰長為25的等腰三角形，實際觀察這些三角形的面積。很顯然，底部越小，面積越小，但為什麼底部30和底部40的三角形面積會相等呢？我說，這面積和底部的關係有點小複雜，或許面積一開始隨著底長而增大，但是大到了某個程度會下降呢！

站在巨人的肩上

我們寫出腰長為25、底長為x的等腰三角形的面積的計算式：

Area(x)=sqrt(25²-(x/2)²)*x/2

前一項是畢氏定理導出的高，不難；不過因為有根號在那裏，比較不好算。我問，這個面積函數的最大值發生在哪裡？

我們可以設法用數學分析得到確切解（analytical solution)。這題用微積分很快就能解出來了，但國中生好像沒有足夠的數學工具來做這件事。這題雖然也可以用代數來解，不過只要題目稍稍變換一下，就得重新解過；雖然是很好的頭腦體操，但不見得實用。

人類不需要一再重複發明同樣的方法、解決同樣的問題，可以站在巨人的肩膀上，挑戰更有意義的新問題。

我說，可不可以幫這個函數做出一張圖？代入一堆數字去畫圖，方法很簡單，但是用手算需要算半天，所以我們很快就喊停。我說，這是古代很多科學家、工程師要做的事情，達文西也要做這些；所以他們為了加速計算，還設計了計算機、計算尺等工具。即使到了人類登陸月球的年代，NASA的工程師們還是得用計算尺來做計算。這是利用數值方法和計算模擬（computer simulation)的解題方法。

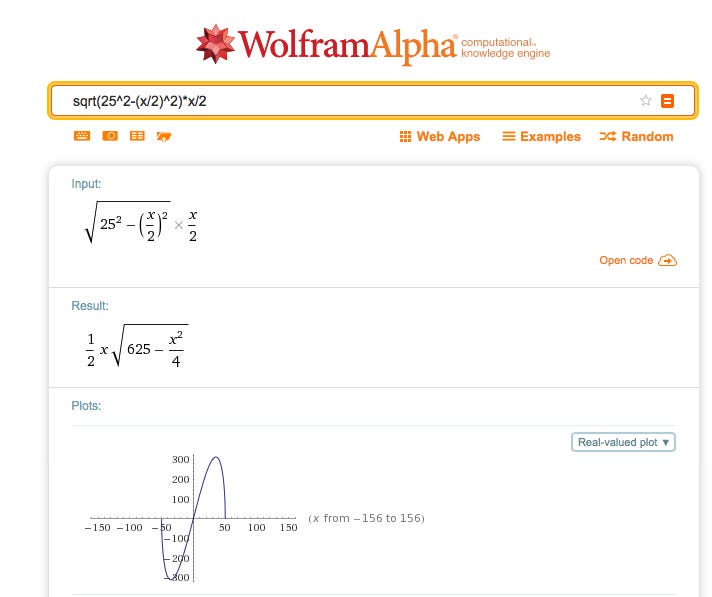
但是我們現在有強大的電腦，為何不用？我們可以寫個程式來計算這個函數？當然可以，二次世界大戰時就是為了計算彈道，研發出真空管電腦。你已經會寫程式了，知道寫段程式來計算很容易；不過有更方便的作法，那就是直接用人家做好的電腦應用服務。

我們上Wolfram Alpha的網站，把計算式打進去，結果馬上畫出圖（見下圖），甚至直接告訴我們最大值出現在25*sqrt(2)。這就是Web service的厲害，人類不需要一再重複發明同樣的方法、解決同樣的問題，可以站在巨人的肩膀上，挑戰更有意義的新問題。解決重複舊問題的價值，會越來越低，因為電腦比你會做這件事。Wolfram Alpha兼具符號運算和數值方法的能力，可得到確切解。

不過，如果沒有基礎，不見得會爬到巨人的肩膀上，就算爬上去也可能站不穩、看不遠。所以很多基礎的東西還是要搞清楚。

科學方法與思維

最後，我談到機器學習。怎麼用機器學習解決以上的問題？我們可以把這個計算式的已知輸入和結果，送進機器學習，再給它新的輸入，看看它會不會回答正確答案？當資料很少的時候，它會和你稍早的瞎子摸象一樣，用過度簡化的模型，做出錯誤的推論。因此資料必須夠多（大數據）、模型夠複雜才行，不過這可能是殺雞用牛刀，但誰知道機器學習的引擎會不會普及廉價到不行呢？

好吧，我承認我不是教數學，我在教計算思維和科學方法。科學有四個重要的方法：實驗、解析、數值模擬、大數據分析，大致都點到了。